上の記事から漏れたこと、あるいはその後勉強して気になったことを寄せ集めた。随時更新予定。ただし現在進行形で勉強しているので、今後内容がガラリと変わる可能性がある。
KdV方程式の一般解
KdV方程式にnソリトン解が存在することはよく理解した。しかしソリトン解の波形の制限は厳しく、KdV方程式に自由に初期値を与えればnソリトン解以外の解が生じることはすぐ分かる。逆散乱法はほぼソリトン解のみを求めるメソッドと化しているから、ソリトン解が何らかの意味で解を尽くしているか(たとえば 空間の正規直交基底になるなど)を問うべきだろう。
偏微分方程式の一般解を考える際は、何か境界条件を課すべきである。本節では ①遠方で急減少なKdV方程式 ②周期KdV方程式 の2つの場合を取り上げよう。
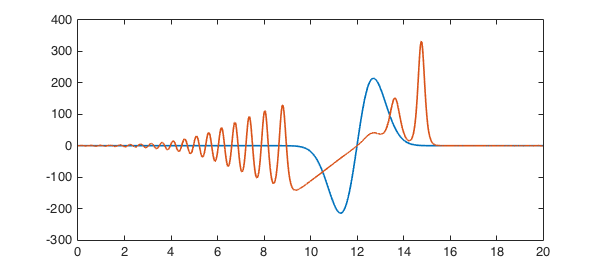
①遠方で急減少する滑らかな任意の解について、十分な時間発展の後で、右に進む多重ソリトンと左に進む多重ソリトンの「重ね合わせ」に漸近することが証明されている(1973年頃)。ゆえにこの境界条件でのKdV方程式に対しては、ソリトン解で本質を掴んだと言ってよさそうだ。無限次元の対称性が一般解に対しても効いている。ただし、ソリトンの「重ね合わせ」の端にはノイズのように小さな「さざ波(ripple)」が観察される。
以上はZabusky-Kruskalの数値実験(1965年)からすでに経験的には知られていたことである。詳細は次の論文を参照。
Grunert-Teschl, “Long-Time Asymptotics for the Korteweg-de Vries Equation via Nonlinear Steepest Descent”, 2008.
②KdV方程式には(超)楕円関数で書ける周期解が存在する。周期解にもnソリトン解が存在し、それは「種数nの超楕円曲線のヤコビ多様体のテータ関数」を利用するものである。周期KdV方程式には(超)楕円関数ソリトンが、①のKdV方程式には指数関数ソリトンがある、と整理しよう。
逆に、アーベル多様体のテータ関数でKP方程式(KdV方程式の親玉)を満たすものは、リーマン面のヤコビ多様体に限られることが知られている(Novikov予想、1986年塩田が解決)。
佐藤スクールによる代数解の分類においても周期解を位置づけることは可能。τ関数の有限次元軌道(無限個の時間変数で動かしたときの軌道が有限次元になるもの)がヤコビ多様体のテータ関数解と対応する。標語的には、「タウのtはテータのt(でもある)」。
なお、①の指数ソリトン解もリーマン面の言葉で書くことができて、通常2重点のみをもつ特異有理曲線に対応する。このτ関数の軌道もやはり有限次元になる。
塩田隆比呂『KP方程式とSchottky問題』1989年
https://www.jstage.jst.go.jp/article/sugaku1947/41/1/41_1_16/_pdf/-char/ja
周期KdVの一般解に対する解析学的なアプローチについて。いくらか調べてみたが、周期KdVに任意初期値を与えたときの長時間漸近解析の結果は見当たらなかった。直感的には、周期条件だと波が空間的に(場合によっては時間的にも)「閉じ込め」られているため、①のようなソリトンへの分解は期待できなさそうである。
『可積分系の歴史』では量子逆散乱法や佐藤スクールの方法など、可積分系の代数的側面に焦点が移行していった。しかしそれらが適用できない一般初期値の場合は、今なお解析学的手法を用いて研究が行われている。
メモA:一般解ではなく特殊解の範疇になるが、KdV/KP方程式のτ関数には③有理関数解も存在する(次の論文や次節のlump-solitonを参照)。これもやはりリーマン面で書けて、通常2重点よりも複雑な特異点を持つ有理曲線に対応する。
有理解なので、遠方で0に漸近したとしても急減少*1は絶対にしない。そのため①と矛盾はしていない。よくよく考えると「急減少」というのは「境界条件」としてはいささか厳しいのだが、このくらい限定しないと指数ソリトンがうまく立ち回ってくれない。非線形性と偏微分方程式と無限次元対称性がせめぎあっている感じがする。
M. Mulase, "Cohomological structure in soliton equations and Jacobian varieties" J. Differential Geom, pp.403-430, 1984.
https://www.math.ucdavis.edu/~mulase/texfiles/cohomological.pdf
M. Mulase, "Algebraic Theory of the KP equations", 1994. https://www.math.ucdavis.edu/~mulase/texfiles/algebraictheo.pdf
Y. Matsuno, "A New Proof of the Rational N-Soliton Solution for the Kadomtsev-Petviashvili Equation", Journal of the Physical Society of Japan, January 15, 1989, Vol. 58, No. 1 : pp. 67-72.
Pierre Gaillard, "Rational solutions to the KdV equation depending on multi-parameters", 2021.
有理関数解/指数関数解/楕円関数解と、いろんなところで見る解の階層がKdV/KP方程式からも確認できた。
メモB:歴史的順序とは逆になるものの、箱玉系を知っている人はそちらでイメージする方が容易い。(周期)KdVの超離散化が(周期)箱玉系で、超離散化の結果ソリトン解しか出てこない。
逆散乱形式としてrigged configuration*2(周期箱玉系の場合トロピカルヤコビ多様体でも可)に移ると時間発展が線形化する。ソリトンを表すパスの空間からrigged configurationへの写像は組み合わせ論的に難しい写像(ないしトロピカルAbel-Jacobi写像)になり、逆の写像が超離散τ関数(ないし超離散テータ関数)になる。以上はKerov-Kirillov-Reshetikhin全単射の箱玉系による解釈にもなっている。
メモC:ソリトン方程式におけるSigma Functionは2000年前後から研究されるようになった対象である。NovikovなどによるKdV方程式の超楕円関数解の表示は実のところ、パラメータが過剰なので、exactな表示には関係式を立てて消去する必要がある。Hirota-Ito(1981)などがこれを実行したが、可能なら最初からexactに表示できた方が良い――というところでSigma Functionが持ち出される。リーマン面の退化に伴うτ関数の変化を扱える点で、テータ関数より精密である。
S. Matsutani, “Hyperelliptic Solutions of KdV and KP equations: Reevaluation of Baker’s Study on Hyperelliptic Sigma Functions”, 2000.
https://arxiv.org/pdf/nlin/0007001.pdf
Nakayasihiki, “Sigma Function as A Tau Function”, 2012.
https://arxiv.org/abs/0904.0846
J. Bernatska, V. Enolski, A. Nakayashiki, "Sato Grassmannian and Degenerate Sigma Function", 2018.
KP方程式の特殊解
前節で見たように、KdV方程式の時点ですでにかなり複雑である。KdVの高次元化であるKP方程式の一般解はなおさら難しい。ここでは特殊解に限っていくつか言及する。
・KP階層のτ関数が無限次元軌道になる場合として、1990年代に行列模型が構成された。[Mulase1994]を参照。
・ロンスキアン解は指数ソリトンを含む、だいぶ広い解のクラス。
・KP方程式のソリトンは、周期解を除くと、とりあえず「lump-soliton」と「line-soliton」の2つを観察できる。
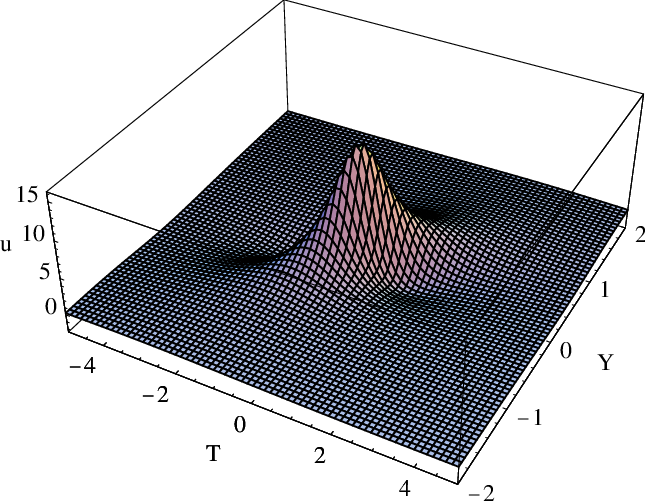
lump(かたまり)型のソリトンは、十分遠方で減少し、τ関数の有理関数解に相当する解である。
A.A Minzoni, N.F Smyth, "Evolution of lump solutions for the KP equation" Wave Motion, Volume 24, Issue 3, 1996, pp.291-305.
line型については次を参照。これは十分遠方でもある領域では0に接近しない、τ関数の指数関数解に相当する解である。
Y. Kodama, "KP Solitons and the Grassmannians: Combinatorics and Geometry of Two-Dimensional Wave Patterns", Springer, 2017.
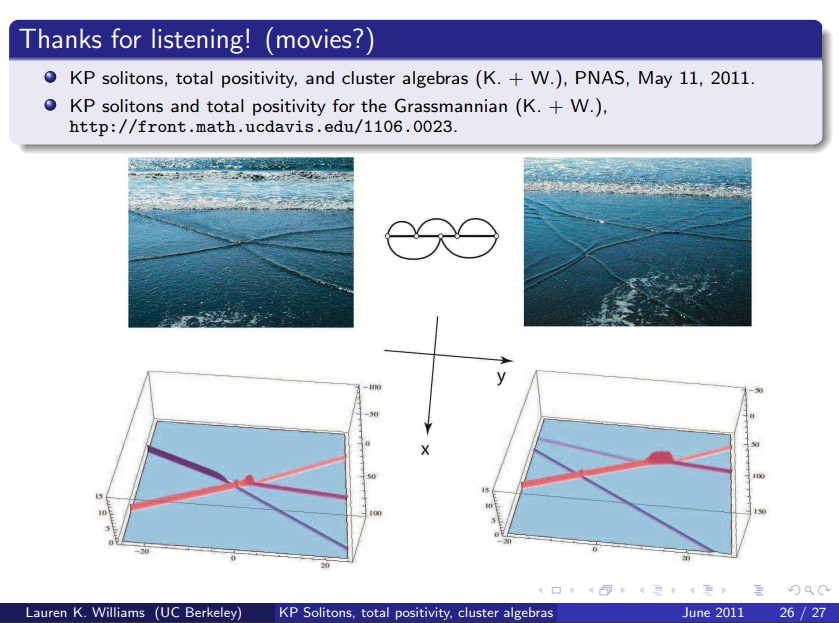
KdVの指数関数ソリトンを高次元化しただけ? いや、空間が2次元なために非自明な「共鳴」が起こる。上図右のグラフで、2つのピンクのソリトンが衝突して振幅がとても大きくなっているあたり、そして次に述べる合流現象に顕著だ。
そもそもソリトンの特徴の1つに擬似的な重ね合わせの実現があった。しかしKP方程式のlineソリトンでは、衝突によってときに「Y字型に合流」してしまう。ただし合流しないこともある。
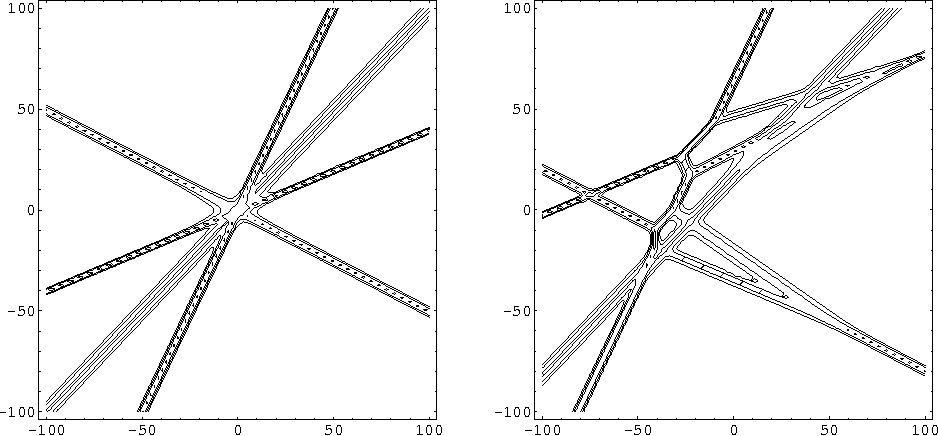
中々大変そうである。line型のソリトンの研究は2000-10年代に、トロピカル幾何やクラスター代数を用いて研究が進んだ。今では代数学的に取り扱うことができる。
可積分系としての共形場理論の謎
『量子群勉強ノート』でも述べたように、可積分系としての共形場理論がよく分からないという話を延々とする。

KZ方程式から
線形微分方程式であるKZ方程式のモノドロミー表現からは量子群のR行列が出てくる(河野-Drinfeldの定理)。これについて色々ツッコミを入れていく。
・古典r行列を積分して量子R行列になるという描像に思える。
・KZ方程式の変数 はアフィンリー代数
のLaurent展開
の不定元
と思っても良い。共形場理論がアフィンリー代数に統制されていることによる。以上2つは[Chari-Pressley]のどこかに書いてある。
・3次元Chern-Simons理論を持ちだしてJones多項式を物理的に解釈したWittenのフレームワークに従えば、モノドロミーがYang-Baxter方程式を満たすことは納得できる(ブレイド群関係式のトポロジカル不変性)。量子群から来ることは漠然とリー型の対称性が生きているとしか……。まあ量子群は自然に出てくるべきクラスだとは思う。
https://member.ipmu.jp/masahito.yamazaki/files/2023/20230318_JMS_proceeding.pdf
・KZ方程式の結果をうまく が1の冪根のときの量子群に拡張して、Kazhdan-Lusztigは標数
の有限次元代数群の既約有理表現と標数
のアフィンリー代数(無限次元!)の既約表現に対応関係をつけた。またテンソル積表現の分岐則も対応することが分かっている。標数が違い次元が違っても対応するのはかなり非自明で奇妙である。「よく分からんが凄い結果」以上の理解は現在の表現論においてされているのだろうか。
柏原、谷崎『Kazhdan-Lusztig予想をめぐって』1995年
https://www.jstage.jst.go.jp/article/sugaku1947/47/3/47_3_269/_pdf/-char/ja
・KZ方程式は数論でも研究されている。
特に1 変数の場合について, その解が 1 変数多重対数関数の形式的級数として, 接続係数がDrinfel’d associator と呼ばれる多重ゼータ値の自然な母関数で書かれることから数論幾何の分野で深く研究されている。
(大井周『形式的KZ方程式の表現と多重ゼータ値の関係式 』2009年)
共形場理論とPainleve性
Painleve性はなんとなく非線形可積分系の背後にあることが分かっている。たとえばアフィンリー代数型のソリトン階層からPainleve性の方程式がそれぞれ出てきたり、2次元Ising模型の有質量臨界極限=ホロノミック量子場で相関関数からPainleve第3方程式 が出てきたりする。だが、共形場理論とPainleveの噛み合わせを見ても可積分系としての理解を助けてはくれなかった。
Painleve方程式には ①動く分岐点を持たない ②モノドロミー保存変形を表す微分方程式 ③ハミルトニアンとτ関数 という3つの見方がある(岡本『パンルヴェ方程式』参照)。
・KZ方程式は確定特異点を持つFuchs型微分方程式なのでモノドロミー保存変形*3を考えることができる、のだがやっているのは見たことが無い。多分面白くないんだと思う(モノドロミー表現は量子群のR行列で面白いのに……)。
・実のところ、KZ方程式はある微分方程式のモノドロミー保存変形の「量子化」になっている。前提知識として、Painleve第VI方程式 の線形特殊解として超幾何関数が出てくることを述べておこう(またPainleve方程式の退化と超幾何関数の合流は
を除き対応する)。この結果の量子化として、量子Painleve方程式の線形特殊解にKZ方程式が存在する。
名古屋創『量子 Painleve 系について』2012年
https://www.kurims.kyoto-u.ac.jp/~kenkyubu/bessatsu/open/B30/pdf/B30_011.pdf
・古典Painleve方程式も共形場理論と関わりがある。 のτ関数は、共形場理論の共形ブロックの無限和(非線形フーリエ変換と思える)で表せる。ここからAGT対応でインスタントン側を見たいらしい。
名古屋創『共形場理論とパンルヴェ方程式』pp.13-28
https://www.sci.osaka-cu.ac.jp/~okado/gakkai/titech19mar_11.pdf
共形場理論の変形
・共形場理論にはさまざまな変形がある。中でも -変形というものは、対称性が
- Virasoro代数になり、相関関数は
- KZ方程式で書けて、モノドロミー表現として楕円量子群のR行列が出てくることが期待されている。その後あんまりうまくいかなかったような話。
P. I. Etingof, I. Frenkel, A. A. Kirillov, "Lectures on Representation Theory and Knizhnik-Zamolodchikov Equations" American Mathematical Society, 1998.
・6頂点模型の相関関数は - KZ方程式で書けることが[Jimbo-Miwa]によって示されている。う~~~ん。あたかも共形場理論が古典系のような扱い。KZ方程式を新時代の超幾何関数と思うなら間違いがない。量子でもあり古典でもある、というのが共形場理論の深さ?
・別の変形として有質量変形(佐藤スクールで言うホロノミック量子場)がある。2次元Ising模型はR行列*4を持つ量子可積分系なので、連続極限であるホロノミック量子場も量子可積分系とみて良いだろう。その無質量極限として共形場理論が出てくる、とも思える。
・共形場理論を変形してソリトン方程式が観察できる例。どちらも対称性がアフィンリー代数だからできなくはないよな、と思う。共形場理論の古典版を考えることと関係がある。
B. Zamolodchikov, ”Integrable Field Theory from Conformal Field Theory”, 1989.
Eguchi-Yang, “Deformations of Conformal Field Theories and Soliton Equations”, 1989.
山田泰彦『共形場理論入門』培風館、2006年
共形場理論とソリトン
・戸田場の理論は古典可積分系だが、量子化すると(うまい方法で量子化すると)共形場理論になる。量子化という作業もヴァリエーションが多い。
・そもそも量子sine-Gordon模型にだってソリトンと呼ばれるものはある。量子-古典対応ってなんなんだ。
松井千尋『可解量子スピン鎖と場の理論 : 散乱行列から共形不変性まで』2017年
https://mercury.yukawa.kyoto-u.ac.jp/~bussei.kenkyu/wp/wp-content/uploads/6100-064215.pdf
・「位相的場の量子論にもPainleve方程式が現れて共形場理論とソリトン理論をつなぐ」(『ソリトンの数理』の「参考書」欄を適宜参照)
S. Cecotti, P. Fendley, K. Intriligator, C. Vafa “A New Supersymmetric Index”, 1992.
・フェルミオン場の共形場理論を使うと、KP階層の準周期解をすべて共形場理論の言葉で書ける。そうしてソリトン方程式の佐藤理論に繋がる。指数τと楕円τを同時に扱える程度の話の気がする。
N. Kawamoto, Y. Namikawa, A. Tsuchiya, Y. Yamada, “Geometric Realization of Conformal Field Theory on Riemann Surfaces”, 1988.
・[DJKM](1983年)より、頂点作用素によってソリトンの数を増やすことができる。だから共形場理論……というのはアナクロニズム。歴史的には、頂点作用素という言葉は79-80年頃のアフィンリー代数の表現論から来ている(物理的実態はもっと前にあったが)。ソリトンも共形場理論もアフィンリー代数で統制されるから頂点作用素の記法が似る、と思った方が良さそう。
共形場理論と量子可積分系
・量子可積分系から共形場理論が出てくるルートとしては、もちろん臨界極限が圧倒的に大事。このとき情報がつぶれてよくわからなくなる。
・ の有理共形場理論(2次元Ising模型の臨界直上の極限として現れる)におけるfusion ringは、
での量子群の傾加群(tilting module)のテンソル則と一致する。Kazhdan-Lusztigがアフィンリー代数と標数
を結び付けたのと同根の現象? なおこの過程で量子次元が
の表現が出てくる。
・Gaudin模型と呼ばれる量子可積分系のある極限は、共形場理論(WZW模型)になる。
武部尚志(述)関谷信寛(記)『可解格子模型と共形場理論の話題から』2006年
共形場理論とゲージ理論
・AGT対応が起こる理由は「6次元 超共形場理論という、ラグランジアンなどが具体的に構成されているわけではないが、状況証拠から存在がほぼ確信されている量子場理論を、2次元と4次元に次元簡約して計算すると、それぞれ2次元共形場と4次元ゲージ理論になる」だった。なんかこう、雑。AGT対応に関してはゲージ理論さんサイドに謎があるような気がする。
結論。可積分系の理論体系における共形場理論の立ち位置がマジでわからん
量子可積分系の中でもっとゆるくとらえるべき? 『ホロノミック量子場』の6章読み直すか?